Class 11 Physics Chapter 6 Work, Energy and Power

.The sign of work done by a force on a body is important to understand. State carefully if the following quantities are positive or negative.

(a) Work done by a man in lifting a bucket out of a well by means of a rope tied to the bucket.
(b) Work done by the gravitational force in the above case.
(c) Work done by friction on a body sliding down an inclined plane.
(d) Work done by an applied force on a body moving on a rough horizontal plane with uniform
velocity.
(e) Work done by the resistive force of air on a vibrating pendulum in bringing it to rest.

Ans.

(a) It is clear that the direction of both the force and the displacement is the same and thus, the work done on it is positive.

(b) It can be noted that the displacement of the object is in an upward direction, whereas the force due to gravity is in a downward direction. Hence, the work done is negative.

(c) It can be observed that the direction of motion of the object is opposite to the direction of the frictional force. So, the work done is negative.

(d) The object which is moving in a rough horizontal plane faces the frictional force, which is opposite to the direction of the motion. To maintain a uniform velocity, a uniform force is applied to the object. So, the motion of the object and the applied force are in the same direction. Thus, the work done is positive.

(e) It is noted that the direction of the bob and the resistive force of air which is acting on it are in opposite directions. Thus, the work done is negative.

Que.2. A body of mass 2 kg initially at rest moves under the action of an applied horizontal force of 7 N on a table with the coefficient of kinetic friction = 0.1. Compute the
(a) work done by the applied force in 10 s.
(b) work done by friction in 10 s.
(c) work done by the net force on the body in 10 s.
(d) change in kinetic energy of the body in 10 s.

Ans: 

The mass of the body = 2 kg

Horizontal force applied = 7 N

Coefficient of kinetic friction = 0.1

Acceleration produced by the applied force, a1= F/m = 7/2 = 3.5 m/s2

Force of friction, f = μR = μmg = 0.1 x 2 x 9.8

Retardation produced by friction, a2 = -f/m = -196/2 = -0.98

Net acceleration with which the body moves,

a = a1 + a2 =  3.5 – 9.8 = 2.5

Distance moved by the body in 10 seconds,

s = ut + (1/2)at2 = 0 + (1/2) x 2.52 x (10)2= 126 m

(a) The time at which work has to be determined is t = 10 s

Work = Force x displacement

= 7 x 126 = 882 J

(b) Work done by the friction in 10 s

W = -f x s = -1.96 x 126

(c) Work done by the net force in 10 s

W = (F – f)s = (7 – 1.96) 126 = 635 J

(d) From v = u + at

v = 0 + 2.52 x 10 = 25.2 m/s

Final Kinetic Energy = (1/2) mv2 = (1/2) x 2 x (25.2)2 = 635 J

Initial Kinetic Energy= (1/2) mu2 = 0

Change in Kinetic energy = 635 – 0 = 635 J

The work done by the net force is equal to the final kinetic energy.

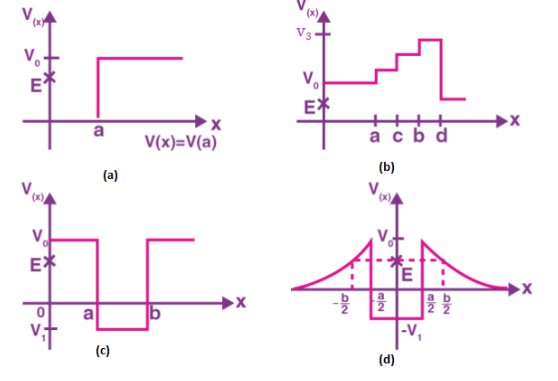
Que. 3. Given in the figure are examples of some potential energy functions in one dimension. The total energy of the particle is indicated by a cross on the ordinate axis. In each case, specify the regions, if any, in which the particle cannot be found for the given energy. Also, indicate the minimum total energy the particle must have in each case. Think of simple physical contexts for which these potential energy shapes are relevant.

Ans:

The total energy is given by E = K.E. + P.E.

K.E. = E – P.E.

Kinetic energy can never be negative. The particle cannot exist in the region where K.E. would become negative.

(a) For the region x = 0 and x = a, potential energy is zero. So, kinetic energy is positive. For x > a, the potential energy has a value greater than E. So, kinetic energy becomes zero. Thus, the particle will not exist in the region x > a.
The minimum total energy that the particle can have, in this case, is zero.

(b) For the entire x-axis, P.E. > E, the kinetic energy of the object would be negative. Thus, the particle will not exist in this region.

(c) Here, x = 0 to x = a and x > b, the P.E. is greater than E, so the kinetic energy is negative. The object cannot exist in this region.

(d) For x = -b/2 to x =-a/2 and x = a/2 to x = b/2 . Kinetic energy is positive, and the P.E. < E. The particle is present in this region.

Que.4. The potential energy function for a particle executing linear simple harmonic motion is given by V(x) = kx2/2, where k is the force constant of the oscillator. For k = 0.5 N m-1, the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of
total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.

Ans. Particle energy E = 1 J

K = 0.5 N m-1

K.E =